Accountants are often providers of information, but what can be done to help them? Matthew Leitch looks at the role information theory could play.
Information theory is not just a vague discussion about information; it is a precise mathematical approach to quantifying information. The intuitive ideas and remarkably simple formulae at the heart of information theory mean it can be usefully applied to functions such as report design and forecast evaluation.
The origins of the theory
A big part of the theory is related to the idea that messages can be compressed to not only make them smaller, but easier to send and store. It is likely that you have seen this at work when zipping a large file to send it by email or upload it. But how much information did the file contain? Was it the 200MB it started out as or the smaller number it compressed to?
According to information theory, 200MB was the theoretical maximum amount of information a file that size could hold. The true information in the file depends on the message itself. A file of random numbers in a random order could be the full 200MB, but a file consisting of the same number repeated millions of times would really contain just a few bytes – enough to say one number many times over.
Shannon imagined a communication channel. This could be a wire carrying electronic signals or a report of financial numbers prepared by an accountant. A series of symbols are transmitted along that communication channel. The information provided by each of those symbols depends on how likely that symbol is when considered from the perspective of the receiver of the message. Usually, the receiver is assumed to be very knowledgeable about the symbols typically transmitted on that channel and is able to take advantage of patterns that make the symbols somewhat predictable.
Crucially, the more surprising the arrival of a symbol is to the receiver, the more information it has provided. In contrast, if a symbol arrives that the receiver was expecting with certainty then it provides no new information at all. The receiver already knew it was coming.
Shannon used an argument based on how you could compress a series of symbols across a communication channel to arrive at the conclusion that the information provided by a symbol received was:
![– logΜ[p] equation](https://www.icaew.com/-/media/corporate/images/technical/business-and-management/bam-magazine/archive/making-use-of-all-your-info-figure-1.ashx?cx=0.5&cy=0.5&cw=1600&ch=520)

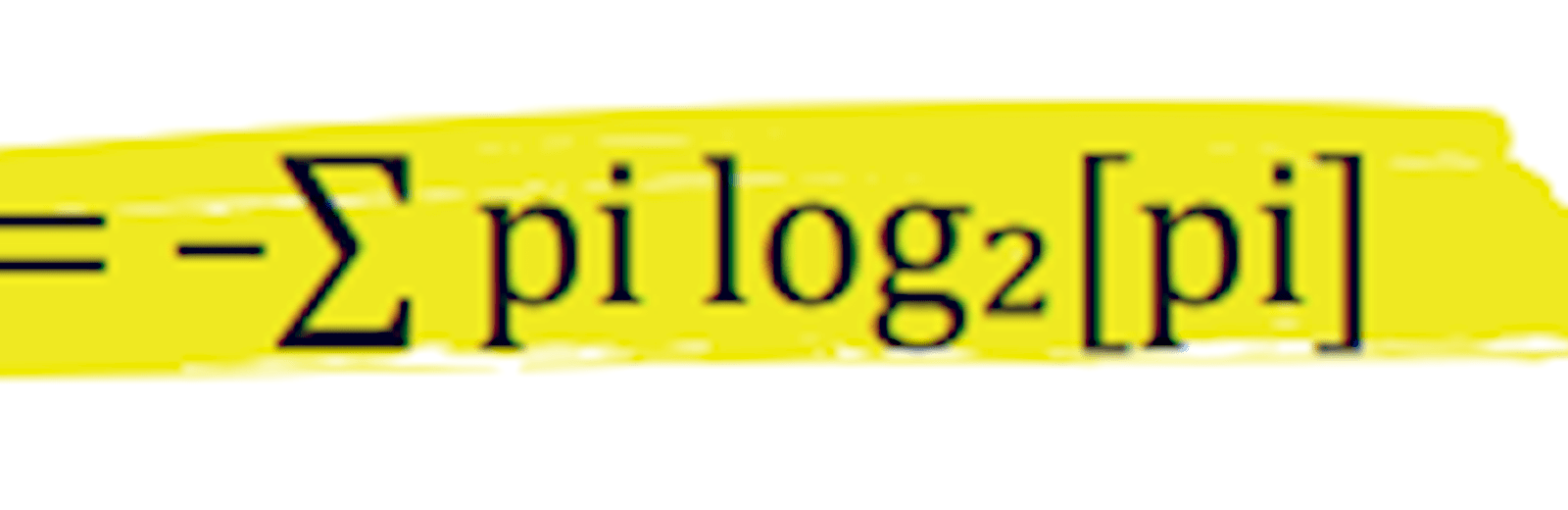
Report design for accountants
Imagine you have a total cost figure that is to be analysed into a list of line items that add up to the total (it’s hard to think of a more traditional form of analysis). Fox suggested interpreting the values of each line item as a relative probability. Divide them through by the total and you get probabilities. Plug them into the entropy formula and you have the quantity of information provided by your report, he proposed.
He concluded that, firstly, the more lines you allowed yourself to analyse the total, the greater the information content of the analysis. Secondly, for a given number of line items, the most information was provided when the analysis divided the total into equal amounts. He demonstrated this by calculating the relative entropy of actual reports, which is simply their actual entropy divided by the highest entropy possible with the same number of line items.
For example, suppose you have a report with space for 10 line items and 90% of the value is on one line, with several of the others having trivial values. Fox argued that it would be better to group some of the tiny items together and use the spare lines to divide up the 90% in an interesting way.
By encouraging accountants to see analyses as something they can revise to provide more information, even if without adding more lines, and suggesting the use of information theory, Fox made an important contribution. Unfortunately, the value of line items is not, in principle, the probability of symbols arriving in a communication channel, so the theory was misapplied.
However, when correctly applied and with sensible assumptions, it turns out that Fox’s conclusions were nearly correct: extra lines do add information.
However, to make best use of the lines you need the unpredictability of each line to be equal, perhaps expressed as the standard deviation of predicted values for them. This unpredictability might be based on past variations, or on the typical or actual balance (as in Fox’s approach). You might also judge unpredictability to be higher for new activities or when environmental change is happening. Another way of looking at it is to choose your analysis to equalise the average budget variances of each line over time.
Of course, a variety of other factors may constrain our choice of line items. Someone else often decides on the headings to use. Also, some items drive important decisions while others do not, perhaps because nothing can be done about them.
Roland Fox suggested that accountants could improve the information content of their reports using entropy calculations
Risk reporting
This makes no sense from an accounting point of view. It is like taking an arbitrary breakdown of your revenue and reporting the top five items as ‘principal revenues’. If you did that the first question would be about how much other revenue is not being reported, while the second, smarter question, would ask why you analysed the revenue in this way as opposed to another way that would have given a very different top five.
Applying accounting techniques and information theory to risk reporting leads to a different interpretation of ‘principal risks’. The challenge is now to divide total risk into categories (the principal risks) so that the total reporting space (a page perhaps) is most efficiently used.
This usually means that all the principal risks have about the same risk level, precisely because the risks were defined that way. Alternatively, if text is provided about the principal risks, then the text can be made proportional to the importance of each risk. Either way, the page space is best used.
This is not the only consideration in deciding how to carve up risk. A breakdown that naturally links cleanly to decisions is also needed, and you might give more space to risks that link to important decisions.
Evaluating forecasts
Kelly is most known for the Kelly criterion strategy and this was part of his proof of an exciting result about information. He derived from Shannon’s formula for information in a different way. Instead of thinking about compressing messages, he used the idea that you can make money from betting with probabilities. But the better the probabilities, the quicker you can make money. He imagined using his betting strategy (which is a good one) and showed that the information content of a message determines how quickly you could make money from it.
This linked information theory to betting and forecasts, but it was decades before people started to get excited by the idea of applying information theory to forecasting. Over the past 20 years or so, meteorologists have triggered a new interest in evaluating forecasts using information theory.
The simplest case is where just a few discrete outcomes are possible. Perhaps the question is whether it will snow or not, or if a big contract will be renewed. A probability forecast is made, which means that each possible outcome is given a probability. For example, there might be a 13% chance of snow with an 87% chance of no snow. When the day comes and we know the truth, it is possible to calculate the ‘surprisal’ of that outcome, given the forecast made. It is:
![– logΜ[p] probability equation](https://www.icaew.com/-/media/corporate/images/technical/business-and-management/bam-magazine/archive/making-use-of-all-your-info-figure-4.ashx?cx=0.5&cy=0.5&cw=1600&ch=520)
Mark Roulston and Leonard Smith, who promoted this idea, called it ignorance (abbreviated to IGN) because this is the extent to which the original forecast falls short of a perfect forecast.
It is not fair to evaluate an individual forecast this way. To evaluate a forecaster (which could be a person, a formula or a piece of software for example), you need many examples of their probability forecasts along with knowledge of what actually happened. You can then calculate the average ING of their forecasts.
In extreme cases, the ING of a forecast that gives a probability of one (certainty) to the outcome that actually happens is zero, while the ING of a forecast that gives a probability of one to an outcome that does not happen is infinite. It is infinite because, with that much certainty, you would in theory feel confident enough to bet everything on that outcome and, when it did not happen, you would lose everything.
This explains the problem with the best estimate for sales next month of £207,000. Taken literally this is saying that the sales figure will be exactly £207,000 and any other outcome will give the forecast an infinite ING, after which it does not matter what happens with other forecasts. This style of forecast is only acceptable because we know that we have to interpret it in a different way. The number £207,000 means a probability forecast in the form of a probability distribution over sales with a mean of £207,000 and a variance that is for the reader to guess. The round number suggests this was rounded to the nearest £1,000 and most readers will think the seven is little more than a hint.
Suppose the forecast is replaced with a probability forecast expressed as a normal probability distribution with a mean of £207,000 and a standard deviation of £3,000. This is fundamentally different from the forecast we looked at before because now there is no list of discrete possible outcomes. The formula that worked for that situation does not fit now. In particular, the normal distribution provides probability densities for particular outcomes, not probabilities.
A number of suggestions have been made for evaluating this kind of forecast using information theory. One of these is the idea of information gain, which represents the extra information provided by a forecast over and above that provided by another, simpler forecast used as a benchmark.
For example, you could use a forecast by simple statistical extrapolation as a benchmark for evaluating expert forecast provided by budget holders. In weather forecasting it is standard practice to evaluate forecasts against the frequency distribution of weather (eg, temperature, rainfall) for the time of year, or ‘climate’. The formula for the information gain of a particular forecast compared to the benchmark is:
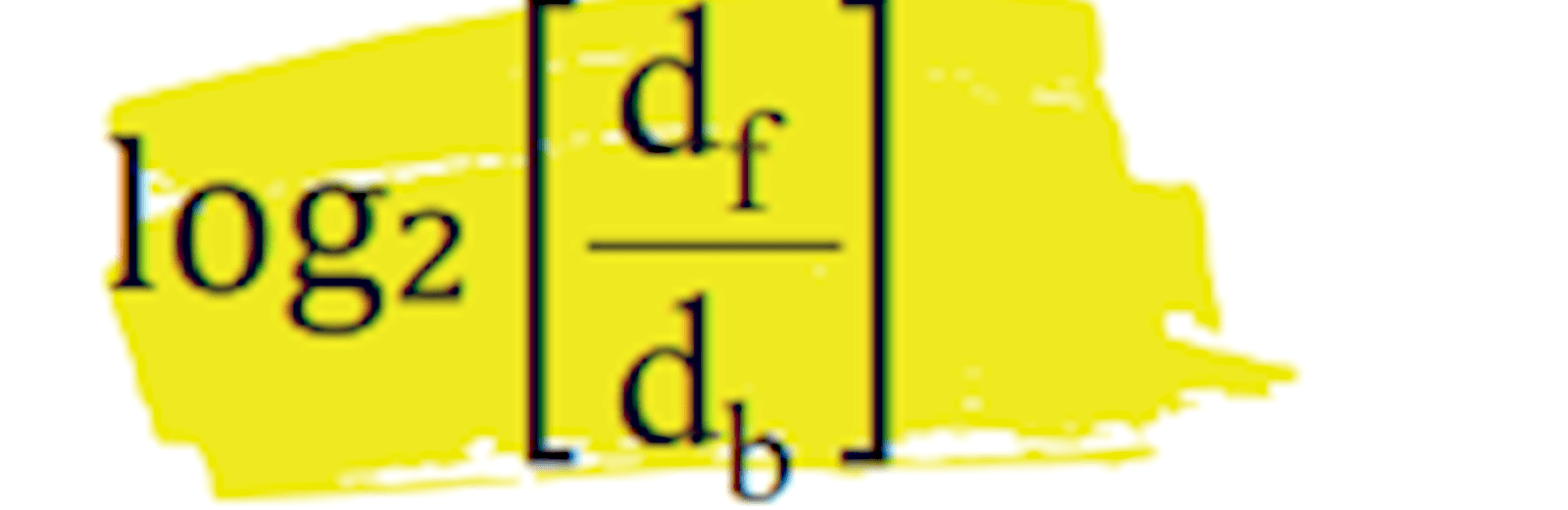
Further reading
The original paper by Claude Shannon is A Mathematical Theory of Communication. Information gain is proposed and nicely explained by Riccardo Peirolo in Information gain as a score for probabilistic forecasts. Both papers are easily found on the web using Google Scholar.
Roland Fox’s book is The Classification and Coding of Accounting Information, published in 1986, but even the second edition published in 1992 by CIMA is extremely difficult to find.
The ICAEW Library & Information Service has a loan copy of the title:
- The classification and coding of accounting information (1st ed.)
- The classification and coding of accounting information (2nd ed.)
For information on borrowing books from the Library please contact us or see our guide to book loans. We offer a free postal loan service for ICAEW members, ACA students and other permitted users.
Download pdf article
Related resources
The ICAEW Library & Information Service provides full text access to leading business, finance and management journals and a selection of key business and reference eBooks.
Further reading on the Kelly criterion strategy discussed in this article is available through the resources below.
You are permitted to access articles subject to the terms of use set by our suppliers and any restrictions imposed by individual publishers. Please see individual supplier pages for full terms of use.
Terms of use: You are permitted to access, download, copy, or print out content from eBooks for your own research or study only, subject to the terms of use set by our suppliers and any restrictions imposed by individual publishers. Please see individual supplier pages for full terms of use.
More support on business
Read our articles, eBooks, reports and guides on Financial management
Financial management hubFinancial management eBooksCan't find what you're looking for?
The ICAEW Library can give you the right information from trustworthy, professional sources that aren't freely available online. Contact us for expert help with your enquiries and research.
-
Update History
- 04 Feb 2019 (12: 00 AM GMT)
- First published
- 03 Nov 2022 (12: 00 AM GMT)
- Page updated with Related resources section, adding further reading on the Kelly criterion strategy discussed in this article. These new articles and ebooks provide fresh insights, case studies and perspectives on this topic. Please note that the original article from 2019 has not undergone any review or updates.

