The very power of statistics has led some to dismiss them as damned lies. Robert Russell talks to Dr Ioannis Kyriakou about how to use them to analyse business performance.
Measures of central tendency - mode, median and mean
Measures of spread - standard deviation and variance
Finance executives comparing sizable sets of data may want to use statistics to quickly carry out their analysis
Distribution
This sounds fine, but how does it help me when all my data sets fall outside the definition of a “normal population”? This is where Chebyshev’s theorem comes in.
Chebyshev's theorem
Applying this to, say, the profitability of businesses would enable us to produce a relative performance score enabling us to identify underperforming divisions. Businesses would be able to say with confidence that 89% of any population would lie inside three standard deviations of the mean. In an audit of output or performance-related pay exercise, a business would be able to better reassure itself of the range of output or to estimate the costs of a programme in advance. Excel can even work out all of these formulae – listed in the example below.
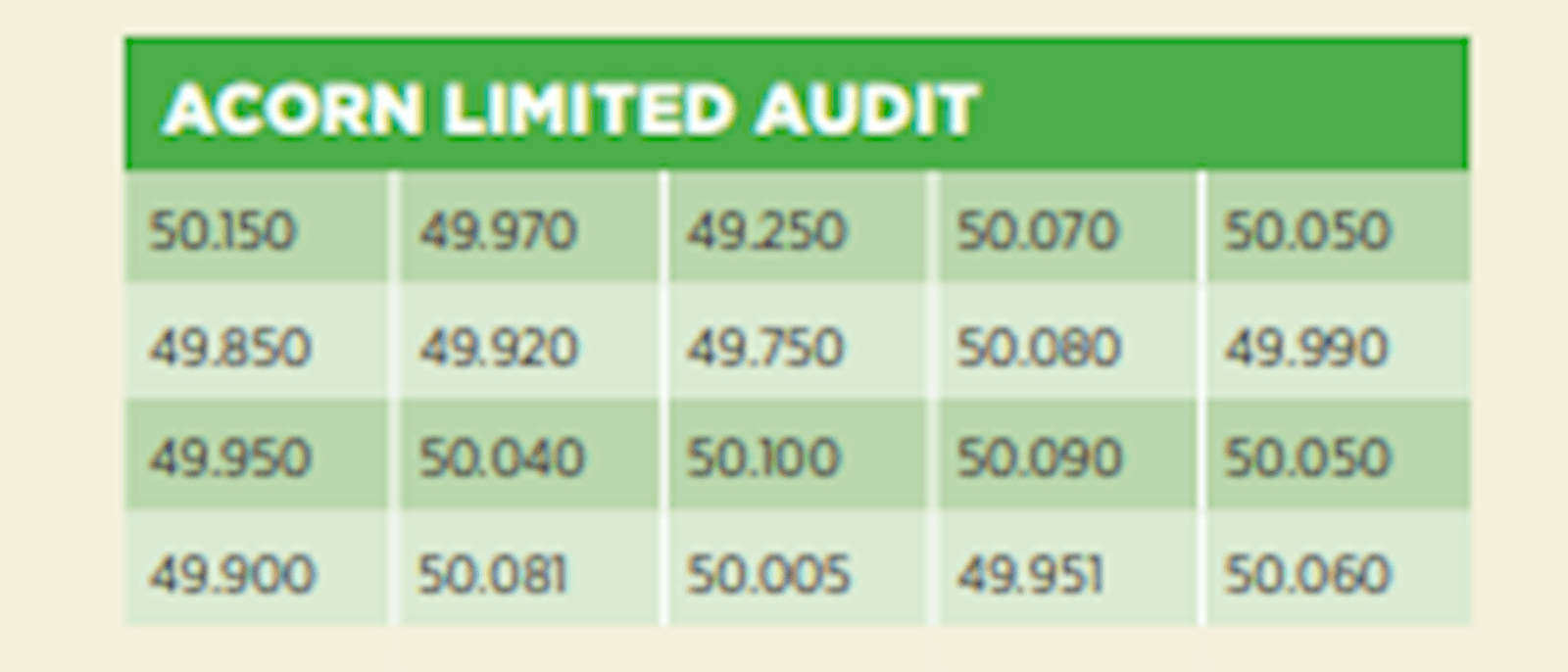
Example
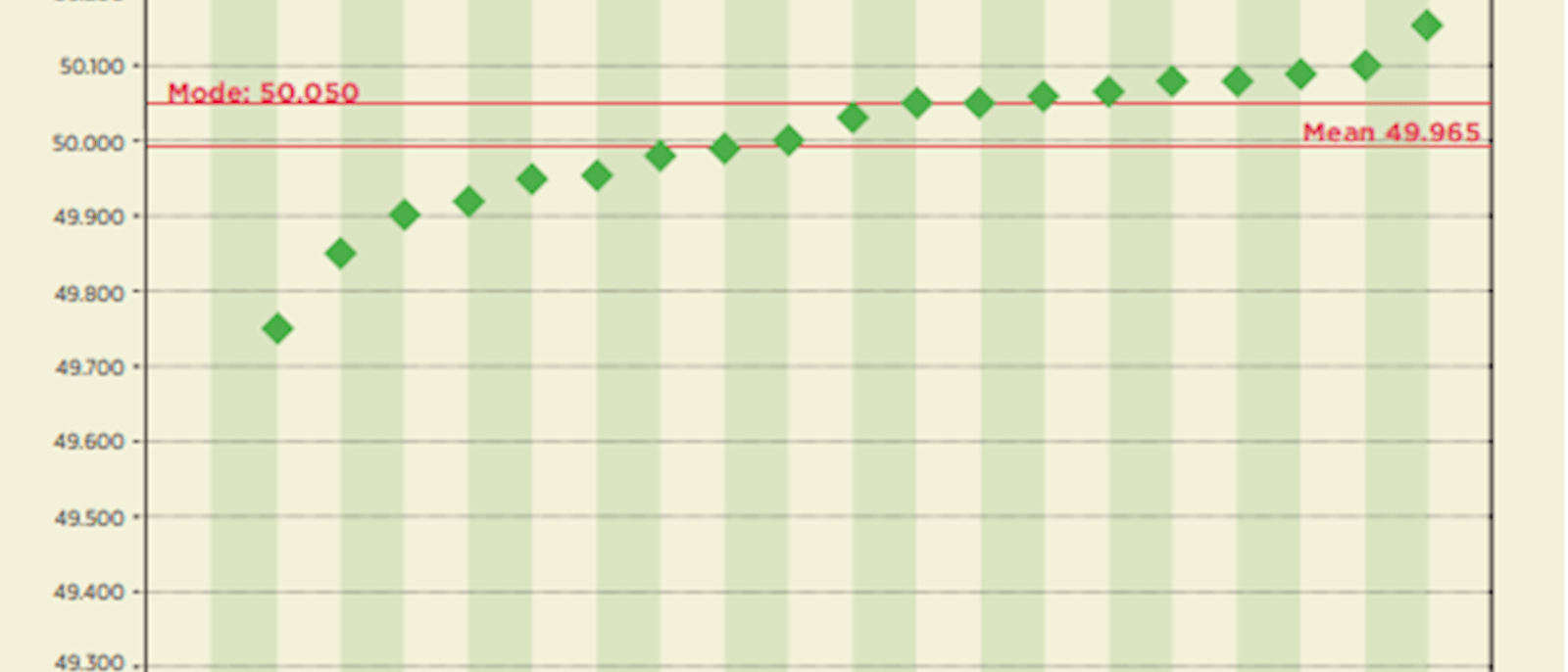
The mean of these results is 49.965 – the Excel formula is @average(a:z) where a:z is the data set. The median score is 50.02 – the Excel formula is @median(a:z) – and the mode is 50.05. Like most data sets this is not a normal distribution.
All three are measures of the “average” weight of a bag of cement, and the company can choose which of them to publish. Reports to customers may want to include all three measures, but there would be nothing statistically wrong about quoting the average weight of each bag as being 50.02kg – the mean bag weight is marginally below 50kg.
We should look at the next step to discover more about the population.
The standard deviation is the square root of the average deviation from the mean, and this is 0.188981 for this population – the Excel formula @stdevp(a:z), where a:z is the data set. Please note that @stdev(a:z) will work out the standard deviation as if the set were only a sample and the result will be different. You should use @stdevp for full data sets.
The mean of 49.965 and the standard deviation of 0.189 (to three decimal points) imply that any weight between 49.776 and 50.154 would be within one standard deviation of the mean, and those between 49.587 and 50.343 would be within two standard deviations of the mean.
What we know with absolute certainty from Chebyshev’s theorem is that 75% of all bagged cement produced will be between 49.587kg and 50.154kg a bag.
The visual form can be seen in Figure 2. Please note that this example is limited for simplicity. We would normally expect any population to have thousands of data points.
Statistics refresher
This is the value seen most often in a population. For unordered qualitative (descriptive, non-numerical) data – such as the types of vehicles passing a census point – the mode is the only representative value. For continuous quantitative (numerical) data, which is that we will be using more frequently, the mode may be meaningless.
MEDIAN
Numerical data sets can be rearranged in order – normally ascending. The middle of the set is the median, and this point can represent the data set, although it is a physical mid-point in a re-ordered population.
MEAN
This is the numerical mid-point of a population and is normally referred to as the average. Although the mean and the median each define, in some sense, the centre of the data, the mean is sensitive to the magnitude of the values on either side of it, whereas the median is sensitive only to the number of values on either side of it. Unusually large or small values affect the mean more than the median.
About the author
Dr Ioannis Kyriakou is a senior lecturer in actuarial science, the Cass Business School, City University
Download pdf article
Further reading
The ICAEW Library & Information Service provides full text access to leading business, finance and management journals.
Further reading on statistics is available through the articles below.
You are permitted to access articles subject to the terms of use set by our suppliers and any restrictions imposed by individual publishers. Please see individual supplier pages for full terms of use.
More support on business
Read our articles, eBooks, reports and guides on Financial management
Financial management hubFinancial management eBooksCan't find what you're looking for?
The ICAEW Library can give you the right information from trustworthy, professional sources that aren't freely available online. Contact us for expert help with your enquiries and research.
-
Update History
- 15 Jul 2015 (12: 00 AM BST)
- First published
- 10 Nov 2022 (12: 00 AM GMT)
- Page updated with Further reading section, adding related resources on statistics. These additional articles provide fresh insights, case studies and perspectives on this topic. Please note that the original article from 2015 has not undergone any review or updates.

